![]()
Examples of the Golden Ratio and the Fibonacci Sequence:
Surprisingly, there are many Fibonacci sequences that can be observed in nature. It occurs so frequently we often hear it being called the 'law of nature'. One of the easiest places to find the sequences is the flower. The number of petals in a flower is often the Fibonacci numbers. (Note that Fibonacci sequence is the following: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 and so on.)

Although flowers with two petals are not common, they exist. Flowers with more petals than shown above will also follow the Fibonacci numbers, even up to 89 petals.
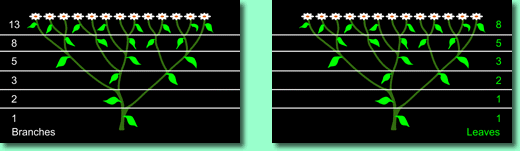
The diagram above shows that if we draw
horizontal lines through the axils, the number of branches and the number
of leaves in each section presents AGAIN the Fibonacci numbers. This also
works for a tree's branches.
There are many other examples shown such as in plants' phyllotaxis, scale
pattern of pine cones, arrangement of seeds in flower heads, and spirals of
pineapples.
The Fibonacci numbers are also related to art and music. In music there are
8 white keys, 5 black keys and 13 black and white keys, and again those numbers
are Fibonacci numbers. Some believe Fibonacci numbers were used in some poetry.
The Golden Ratio.
The Golden Ratio has been used in art
and architecture for a long time.
The main idea is this:
A M B
| 1-x | x |
The ratio of 1-x to x is the same as the ratio of x to 1
1 - x = x which simplifies to 1-x = x2 x 1This gives two values for x, (-1-Ö5)/2 and (Ö5-1)/2.
The first is negative, so does not apply here. The second is just phi (which has the same value as 1/Phi and as Phi-1).
This ratio makes things look beautiful and is identified in many art works. One reason for the exquisite beauty of the Mona Lisa, for example, may be due to the fact that the golden ratio is used in her face.
It is also used in paper such as post cards in order to make it look beautiful. You can start with a golden ratio rectangle and make a smaller golden ratio rectangle inside, making the previous shorter side the longer side, and repeating the procedure. Drawing quarter circles inside each rectangle you'll get a spiral which is often identified in snail shells or the galaxies.

A Controversial Issue
There are many books and
articles that say that the golden rectangle is the most pleasing shape and
point out how it was used in the shapes of famous buildings, in the structure
of
some music and in the design of some famous works of art. Indeed, people such
as Corbusier and Bartók have deliberately and consciously used the
golden section in their designs.
However, the "most pleasing shape" idea is open to criticism. The golden section as a concept was studied by the Greek geometers several hundred years before Christ, as mentioned on earlier pages at this site, But the concept of it as a pleasing or beautiful shape only originated in the late 1800's and does not seem to have any written texts (ancient Greek, Egyptian or Babylonian) as supporting hard evidence.
At best,
the golden section used in design is just one of several possible "theory
of design" methods which help people structure what they are creating.
At worst, some people have tried
to elevate the golden section beyond what we can verify scientifically.
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html