 |
|
 |
GOLDEN POLYGONS
The golden ratio is the
number (1 + Ö5/)2. A golden rectangle
is a rectangle with width w and length d such that w/d or d/w is equal to
(1+ Ö5)/2.
As pointed by Neil, Eric and Geoff (St Peters), the golden rectangle is
an aesthetically pleasing shape and has been used by architects and artists
to enhance the natural beauty
of their work. However, there are many more “golden shapes” which
enhance nature’s beauty, for instance golden hexagons are being used
by plastic surgeons to create the “perfect face”.
Below we will show you how to construct some of these shapes.
You will need a pencil, ruler and compass.
|
|
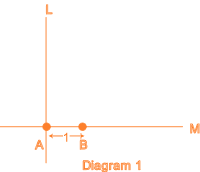
Draw a line M containing two points - A and B. The points A and B are a distance of 1 unit apart. At the point A, draw a Line L perpendicular to M. (Diagram 1) |
|
|
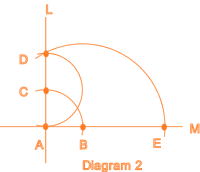
With
compass point at A, draw an arc through point B. The point of intersection of the arc with line L, is labelled C. With compass point at C, draw an arc through point A. The point of intersection of the arc with line L is labelled D. With compass point at B, draw an arc through point D. The point of intersection of the arc with line M, is labelled E. (Diagram 2) |
|
|
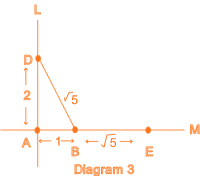
Note that the
right-angled triangle DAB, has side AB of length 1 unit,
side AD of length 2 units and so side DB is of length
Ö5, and AE is of length |
|
|
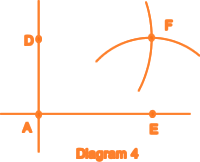
With
compass point at E, draw an arc of radius the length of AD,
and with the compass point at D draw an arc of radius the length
of AE. Label the intersection of these two arcs F. (Diagram 4) |
|
|
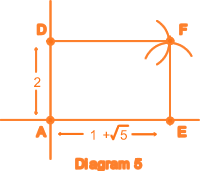
Draw
a line segment from D to F and a line segment from E
to F. Now AEFD is a golden rectangle. (Diagram 5) |
|
|
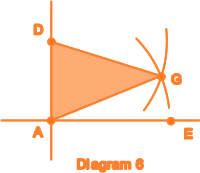
Return
to Diagram 4. Draw two intersecting arcs of radius the length of AE. One with compass point at point A and the other with compass point at point D. Label the point of intersection G. The triangle ADG is a golden triangle; it is an isosceles triangle with the ratio of the longer side (1 + Ö5 units) to the shorter side (2 units) equalling the golden ratio. (Diagram 6). |
|
|
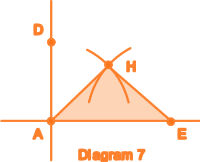
Alternatively you may construct a golden triangle by drawing two arcs of radius length AD, one centred at point A and the other centred at point E. Label the point of intersection of the arcs H. (Diagram 7) |
|
Golden Pentagons
|
|
|
|
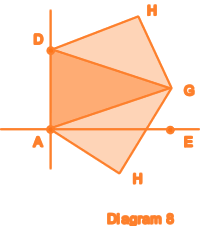
To
construct a golden pentagon we place a copy of the triangle AHE
on the longer sides of the triangle AGD. (Diagram 8) |