Expokit

Home | Download | Support
Understanding Expokit

Fundamentals

The solution of the problem

{
{
{
{
{

dw(t)
dt
=
Aw(t) + u,
t in [0, T]

w(0)
=
v,
initial condition.

(1)
is known to be
w(t) = etAv + tphi(tA)u.
(2)
where phi(x) = (ex-1)/x.

When u = 0, the solution is simply w(t) = exp(tA)v. Expokit provides user-friendly routines (in Fortran 77 and Matlab) for addressing either situation (case u = 0 and case u neq 0). Routines for computing small matrix exponentials in full are provided as well. The backbone of the sparse routines consists of Krylov subspace projection methods (Arnoldi and Lanczos processes) and that is why the toolkit is capable of coping with sparse matrices of very large dimension. The package handles real and complex matrices and provides specific routines for symmetric and Hermitian matrices. When dealing with Markov chains, the computation of the matrix exponential is subject to probabilistic constraints. In addition to addressing general matrix exponentials, a distinct attention is assigned to the computation of transient states of Markov chains.

The purpose of this cursory introduction is to let the reader catch a glimpse of the fundamental elements that make Expokit so fast and robust. The large sparse matrix exponential situation (case u = 0) is taken as the basis of the exposition.

To compute w(t) = exp(tA)v, the Krylov-based algorithm of Expokit purposely sets out to compute the matrix exponential times a vector rather than the matrix exponential in isolation.

Given an integer m, the Taylor expansion

w(t) = etAv = v + (tA)
1!
 v + (tA)2
2!
 v + ...
(3)
can be truncated at order m-1, thereby yielding a polynomial approximation of degree m-1
c0v + c1(tA)v + c2(tA)2v + ... + cm-1(tA)m-1v
with coefficients {ci = 1/i!} that approximates the vector. However these are not necessarily the best coefficients and one can set out to look for a better linear combination (viz. polynomial). All polynomial approximations of degree at most m-1 (including therefore the truncated Taylor polynomial as well as the optimal polynomial approximation) are elements of the Krylov subspace of dimension m, defined as
Km(tA,v) = Span{v, (tA)v, ..., (tA)m-1v}.
(4)
Hence it is more general to state the problem as that of finding an element of Km(tA,v) that approximates w(t).

[V,H,beta] = arnodi(A,v,m)
beta := ||v||2
v1 := v/beta;
for j := 1:m do
      p := Avj
      for i := 1:j do
            hij := viTp
            p := p - hijvi
      end
      hj+1,j := ||p||2
      vj+1 := p/hj+1,j
end
Elements of the Krylov subspace are better manipulated via their representation onto an orthonormal basis. The Arnoldi procedure outlined on the right is a convenient procedure which constructs such a basis. This procedure is mathematically equivalent (but numerically superior by far) to the Modified Gram-Schmidt procedure over the power sequence [v, (tA)v, ..., (tA)m-1v].

From the starting vector v, if the Arnoldi procedure is applied simply with A (rather than tA), then upon completion it builds two matrices

Vm+1 = [v1, v2, ..., vm+1] in Rn×(m+1)
and
H
 
 = [hij] in R(m+1)×m
satisfying the fundamental relations:

AVm
=
Vm+1 
H
 
 = VmHm + hm+1,mvm+1emT
(5)
VmTAVm
=
Hm.
(6)

For j = 1, ..., m+1, the subset Vj = [v1, ..., vj] in Rn×j is an orthonormal basis of Kj(A,v), i.e., VjTVj = I. The first basis vector v1 is the normalized v so that in particular v = betaVme1, where beta = ||v||2, ei is the i-th unit basis vector and throughout this exposition, it is assumed that its length is defined acccording to its context.
The matrices 
H
  
 and  Hm   have a special form
H
 
 = [
[
[
[
[
[
[


Hm

0 ... 0 hm+1,m

]
]
]
]
]
]
]		 in R(m+1)×m;   Hm = [
[
[
[
[
[
[
[
[
h11
h12
h13
...
h1m
h21
h22
h23
...
h2m

···
···

:


···
···
:

0

hm,m-1
hmm

]
]
]
]
]
]
]
]
] 		in Rm×m
Hm = VmTAVm is a Hessenberg matrix (i.e., triangular with an extra sub-diagonal) and it represents the projection of the operator A onto the Krylov subspace with respect to the basis Vm.

For any arbitrary scalar tau, Km(tauA,v) = Km(A,v), and in fact, multiplying (5) and (6) by tau shows that it is straightforward to extend these relations to tauA using tauHbar and tauHm with Vm+1 unchanged. Hence there is no loss of generality when applying the Arnoldi procedure directly to A.

These key observations are vital to the overall Krylov solution technique.

Let wopt be the optimal Krylov approximation in the least squares sense to w(tau) = exp(tauA)v. Since Vm is a basis of the Krylov subspace, wopt = Vmyopt with yopt in Rm. Thus by defintion we have

||wopt - w(tau)||2 =
min
x in Km(tauA,v) 
 ||x-w(tau)||2 =
min
y in Rm 
 ||Vmy - w(tau)||2.
The linear least squares problem defined by the last expression is full-rank and it is well-known that its solution yopt can be stated in terms of Vm+ (the Moore-Penrose inverse of Vm) as
yopt = Vm+w(tau) = (VmTVm)-1VmTw(tau) = VmTexp(tauA)v.
Using the fact that v = betaVme1, it follows that
wopt = Vmyopt = betaVm(VmTexp(tauA)Vm) e1.
This relation characterizes the optimal approximation but it is awkward since it requires exp(tauA). However, we may approximate VmTexp(tauA)Vm by exp(tauVmTAVm). In other words, the projection of the exponential operator exp(tauA) with respect to the basis Vm is approximated by the exponential of the projection of the operator tauA with respect to the same basis. Now recall (6), we then end up with the approximation
exp(tauA)v approx betaVm exp(tauHm)e1.
(7)
Moreover, we can make further use of the ingredients computed by the Arnoldi procedure to define an improved approximation
exp(tauA)v approx betaVm+1 exp(tau
H
 
 m+1)e1
(8)
where
H
 
 m+1 = [
H
 
 |  0] in R(m+1)×(m+1). 
Thus the distinctive feature in these Krylov approximations is that the original large problem of size n is converted to a small problem which is more desirable (usually m << 50 whilst n can exceed many thousands). The computation of the reduced-size problem is done with classical dense methods, such as the Padé method. The mathematical basis of these approximations has been documented [Gallopoulous and Saad, Lubich et al., Philippe and Sidje]. In particular, Saad has shown that these are indeed polynomial approximations. Specifically,
betaVmexp(tauHm)e1 = pm-1(tauA)v
where pm-1 is in fact the Hermite interpolation polynomial (of degree m-1) that interpolates the exponential function at Eig(tauHm), the set of eigenvalues of tauHm, and
betaVm+1exp(tau
H
 
 m+1)e1 = pm(tauA)v
where here pm is the Hermite interpolation polynomial (of degree m) that interpolates the exponential function at Eig(tauHm) union {0}.

It is known from the theory of matrix functions that exp(tauA)v = pn-1(tauA)v where pn-1 is the Hermite interpolation polynomial of the exponential function at Eig(tauA). From the theory of Krylov subspaces, Eig(tauHm) not only approximates a larger subset of Eig(tauA) as m increases but also approximates it more accurately. These results further provide a stimulus for using these approximations. In our implementation, we use the corrected approximation (8) exclusively.

Numerical example

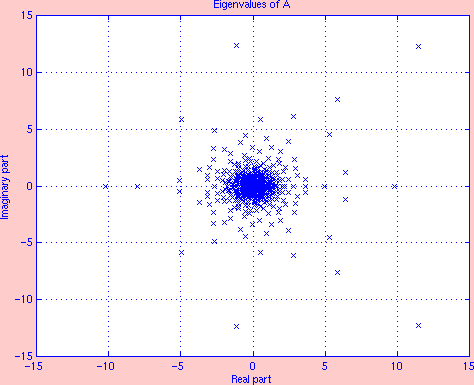Spectrum
Spectrum

Errors
Errors

For a random v and A of order 500 whose spectrum Eig(A) is given on the first figure, the second figure shows three error curves corresponding to ||wexact - wmthapprox||2, with wexact = exp(A)v and wmthapprox is either the m-th degree optimal approximation, the m-th degree Krylov approximation in (8), or the m-th degree truncated Taylor approximation. As m gradually increases from 1 to 30, the optimal error and the Krylov error decrease significantly from 106 to 10-6.

As illustrated graphically, this relatively easy to get Krylov approximation is not the optimal one but as m augments, it quickly draws close to the optimal and it is better than the m-fold Taylor expansion - which highlights that for the same amount of matrix-vector products, the Krylov approximation is better than the Taylor approximation. However, the Krylov approach needs more room (especially to store V in Rn×(m+1)) and involves more local calculation (notably the Arnoldi sweeps needed to construct V and Hbar). Hochbruck and Lubich have shown that the error in the Krylov approximation behaves like O(e-tau||A||2[(tau||A||2e)/ m]m) when m geq 2tau||A||2.

Krylov approximation
Computes w(t) = exp(tA)v

w := v;
tk := 0;
while tk < t do
      [V,H,beta] = arnoldi(A,w,m)
      repeat
            tau := stepsize;
            w := betaVexp(tauH)e1;
            errloc := local error estimate;
      until errloc <= 1.2tol;
      tk := tk + tau;
end

Step-by-Step Integration

Given that in reality t||A|| can be large, w(t) = exp(tA)v is not computed in one go. Instead, as shown below, a step-by-step integration similar to that of a standard ODE solver is used:

{
{
{
w(0)
= v
w(tk+1) = w(tk+tauk) = exp((tk+tauk)A)v = exp(taukA)w(tk)

(9)  
where
k = 0, 1, ..., s,      tauk = tk+1-tk,     0 = t0 < t1 < ... < ts < ts+1 = t.

Consequently, in the course of the integration, one can output intermediate discrete observations (if they are needed) at no extra cost. The {tauk} are step-sizes that are selected automatically within the code to ensure stability and accuracy. This time-stepping selection is done in conjunction with error estimations. Nevertheless it remains clear from (9) that the crux of the problem at each stage is an operation of the form exp(tauA)v, albeit with different tau's and v's. The selection of a specific step-size tau is made so that exp(tauA)v is now effectively approximated by (8) using information of the current Arnoldi process for the stage. Following the procedures of ODEs solvers, an a posteriori error control is carried out to ensure that the intermediate approximation is acceptable with respect to expectations on the global error. Further information and references may be obtained from the Expokit documentation.