by Dr Phil Pollett

Have you ever wondered why birds flock or fish swarm? Did they cooperatively look at the map before they started, or are they instinctively following the school captain? As your teacher will tell you, flocking can be achieved by the individuals obeying very simple rules: follow those ahead of you, stay close to those near you, but do not bump into them. Search the www on “Boids” and you will find computer simulations of flocking that are generated from a set of simple rules. Flocking is an example of an “emergent behaviour” because it is the net result of the actions of individuals, yet the behaviour is not “coded” into any one individual. Interestingly, emergent behaviour is a feature of many complex systems.

One technique for simulating complex systems and studying emergent behaviour is the cellular automaton. A cellular automaton consists of a regular grid of cells. The state of each cell evolves in discrete time steps according to a set of rules based on the states of neighbouring cells. (See Infinity 5 for cellular automaton which model the coral reef, or the back page of this issue for Conway’s Game of Life.) Even when the state is as simple as ON or OFF, cellular automata can produce the kind of complex behaviour that has led some scientists to speculate that much of what we observe in our universe can be explained in this way (this is the central thesis of Stephen Wolfram’s book A New Kind of Science).

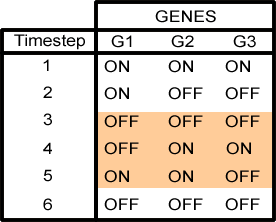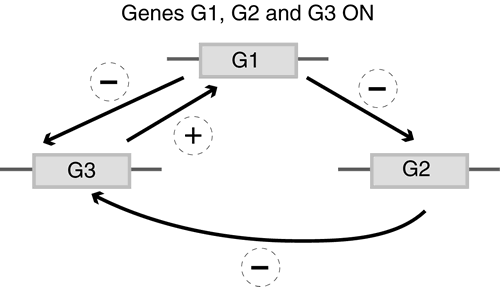
A similar approach can be used to model the interaction of genes. To see how this may work, assume that we have a system of three interacting genes, labeled G1, G2 and G3. Also assume that a gene is either ON or OFF, but nothing in between. In our example, if G1 is ON it inhibits (switches OFF) G2 and G3. If G2 is ON it inhibits G3. If G3 is ON it activates (switches ON) G1. The diagram below may be used to represent this system. If G1 is not being activated by G3 it switches OFF. If G2 and G3 are not being inhibited they activate (switch ON). If we set each gene to an initial state, i.e. either ON or OFF, then a model showing a step-by-step change over time can be developed.

Suppose for instance, that initially all the genes are switched ON; then the behaviour pattern, shown above, evolves. Such models can be easily “evolved” on a computer for thousands of steps.

Various patterns emerge. In many cases the behaviour sequence enters a loop, continually repeating itself, meaning it is cyclic. In the above example Steps 3, 4 and 5 will continually cycle around. Somewhat surprisingly more complex, even chaotic, behaviour patterns can emerge from a few simple rules.

More recently researchers have been experimenting with “biomorphs”, which are computed visual representations of a set of “genes”.
The new twist is to include a random mutation in the simple set of rules, an idea derived from Darwin’s theory of evolution. This can lead to the evolution of other interesting complex forms. (Search the www for “Biomorphs” and you will soon be creating your own new life forms. Search on “Artificial life” to learn where the ideas of Richard Dawkins are now leading.)

Dr Phil Pollett is a Reader in Mathematics and Director (Qld) of the ARC Centre of Excellence for Mathematics and Statistics of Complex Systems. His work is concerned with developing mathematical models for complex biological phenomena, telecommunications systems, epidemics and chemical processes.