![]()
 |
 |
The Golden Section is a mathematical constant ratio, 1:1.6180339..., it appears in nature and was discovered by Pythagoras in the 5th century. The Fibonacci Sequence, 1,1,2,3,5,8,13,21..., is closely related to the Golden Ratio. The ratio of each term to the previous one gradually converges to a limit of approximately 1.618, which is the same values as the Golden Ratio.
Architecture:
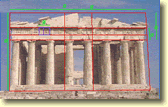 |
In architecture, we can recognise the Golden Ratio, height:width, from the frontage of the Parthenon which is a famous ancient Greek temple. The specialists have reckoned that the golden rectangle shape appeals miraculously to the eye. This is the reason this proportion is still used in contemporary architecture and industry. |
| In the case of the Pyramids, the Golden Ratio was important for the Egyptians as not only a mathematical proportion but also a sacred ratio in their religion. We can assume that there is a right angle triangle when we see it from the side and the ratio that hypotenuse and base make is the Golden Ratio. It has, consequently, a base angle of approximately 60o and a vertex angle of approximately 30o. | |
Art:
 |
We can also find the Golden Ratio Leonardo Da Vinci's art. If we see the disposition of objects in his pictures as well as the frames, the proportion of two lengths of blanks (left and ride side of the object) is the Golden Ratio, which make them more pleasing to the eye. The man's arm in the has the Golden Ratio to his entire arm-span. |
Nature:
 |
|
Nautilus seashells and galaxies
in nature represent the Golden Ratio as well as the Fibonacci Sequence.
If we keep making squares from the golden rectangle and indicate an
arc or if we directly draw lines which are the same values of Fibonacci
Sequence numbers perpendicularly, these two methods, eventually, give
us the same shape of the natural things above. |
Music and Poetry:
In music there are the 5-tone scale (the black notes), the 8-tone scale (the white notes) and the 13-tone scale (the complete octave) which are Fibonacci Sequence numbers on the piano. Many can be divided into two sections as the Golden Ratio has been found from Mozart and Beethoven's music and some rhythm or rhyme in poems. Perhaps these play sound more pleasing to the ear.
Mathematics:
Prime numbers, random numbers, factorisation properaties and Pascal's Triangle are all related to the Golden Ratio and the Fibonacci Sequence mathematically.