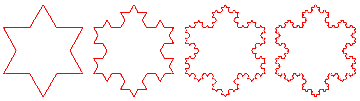
Constructing a Koch snowflake is a step by step process.

Start with an equilateral triangle — side length 1,
perimeter length 3.

Step1
Think of each side as a line segment and replace each line segment by one that has a kink in it. The kink must be in the shape of two sides of an equilateral triangle. So to construct it put an equilateral triangle side length 1/3 in the middle of the line segment and then delete its base.
Your figure is now made up of 3x4 line segments each with length 1/3 and the perimeter has length 3x 4/3.

Step2.
Repeat the same process for each line segment. Your figure is now made up of 3x4x4 line segments each with length 1/9 and the perimeter now has length 3x4/3x4/3.

Step 3.
Perimeter length is 3x4/3x4/3x4/3.
At each step a straight line segment of length a goes to a kinked one with length 4a/3.So after n steps the perimeter length is 3(4/3)^n

What happens as we let n tend to infinity?

Since 4/3>1, (4/3)^n goes to infinity. The perimeter has infinite length!

See also:
http://math.rice.edu/~lanius/frac/koch.html
and
http://www.shodor.org/interactivate/activities/koch/what.html