![]()
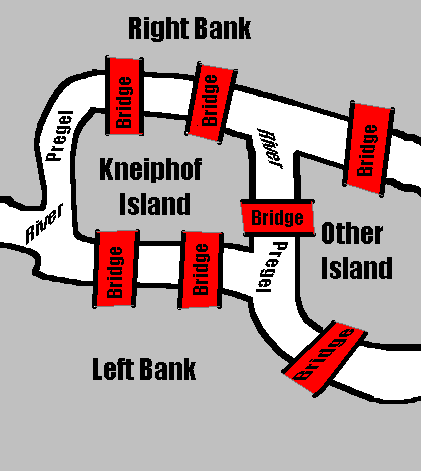
| The German town of Königsberg
was built on both sides of a river. The town included two islands connected to the shores and each other by a series of seven bridges. The question posed by Euler was whether residents of Königsberg could take a stroll in the evening during which they would cross each of the seven bridges exactly one time. |
 |
|
To answer this question, Euler mathematized it, that is, he took the essential elements of the situation and represented them using mathematical objects. In this case he used segments of lines and curves and their points of intersection. |
|
| Below is a schematic
map of the bridges across a river. In fact it is a rough map of the seven
bridges of Konigsberg, the home town of Leonard Euler in 1736. Can you work out a route through the town crossing each bridge precisely once? |
|
 |
|
|
Euler proved that
you can't!
|
|
| Think of the map as a network. Can you draw it without raising your pen or retracing your steps? | |
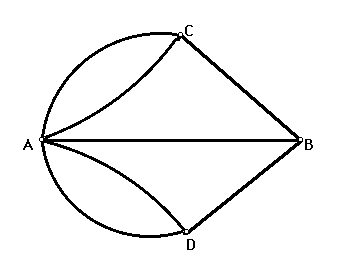 Euler showed that if there are more than two vertices (A,B,C or D) with an odd number of paths to or from them, you can't do it! |
|
