Chapter Seven 

Functions

Section 7.1

The Definition of a Function

The following solutions make use of information found on pages 344 - 354 of the textbook.

Exercise 7.1.1:  Definitions

Fill in the blanks to complete the following sentences.

  1. A function f from a set X to a set Y is a relation from the set X to the set Y with the property that each element of X is related to a unique element of Y.
  2. The notation  f: X implies.jpg (563 bytes) Y is read f is a function from X to Y.
  3. The definition of a function f: X implies.jpg (563 bytes) Y states that given an element x in X, there is a unique element y in Y that is related to x. We write y = f(x), read y equals f of x.
    We say x is mapped under f to y or we say f sends x to y and write x farrow.jpg (608 bytes) y or x implies.jpg (563 bytes) f(x).
    We can think of x as the input and y as the related output.
    Equivalently, the value of f at x is denoted f(x) and the image of x under f is denoted f(x).
  4. The domain of the function f: X implies.jpg (563 bytes) Y is the set X and the co-domain of the function f is the set Y.
  5. The range of a function f: X implies.jpg (563 bytes) Y is the set of yin.jpg (890 bytes)Y such that y = f(x) for some xin.jpg (890 bytes)X. Symbolically the range of f is:
    { y inred.jpg (890 bytes)Y | y = f(x), for some x in X}.
  6. Given a function f: X implies.jpg (563 bytes) Y and an element yin.jpg (890 bytes)Y, the inverse image of y is the set of all elements xin.jpg (890 bytes)X such that f(x) = y. Symbolically the inverse image of y is:
    { x inred.jpg (890 bytes)X | f(x) = y}.
  7. An arrow diagram for a function has the following two properties:
    1. Every element of X has an arrow coming out of it;
    2. No element of X has two arrows coming out of it that point to two different elements of Y.
  8. Suppose f and g are functions from a set X to a set Y. Then f equals g, written f = g, if, and only if, f(x) = g(x) for all xinred.jpg (890 bytes)X.
  9. The special function iX from the set X to X is called the identity funtion on X and for all  x in.jpg (595 bytes) X,  iX(x) = x.
  10. Previously we said that a sequence was a list of elements. More formally, a sequence is a function whose domain is the set of integers that are greater than or equal to a particular integer. (See page 349 of your textbook for an example of this.)

 

Exercise 7.1.2:  Examples

You should attempt all these exercises yourself, using the textbook as an aid. Once you have attempted each question, check your answers by following the appropriate links. If you are stuck on a question, choose the link that gives you a hint and then try the question again.

1. Let f be the function defined by the arrow diagram below:
S7_1_1.jpg (6814 bytes)

a) Write down the domain and co-domain of f.

b) Find f(1), f(2) and f(3).

c) What is the range of f? 

d) Find the inverse images of a, b and c.

Full solution

2. Which of the following define functions? Explain your answer.

a) b)

S7_1_2a.jpg (6728 bytes)

S7_1_2b.jpg (6977 bytes)

Hint
Full solution


3.a) Define functions f : Rimplies.jpg (563 bytes)R and g : Rimplies.jpg (563 bytes)R, where   f(x) = x for all  xin.jpg (595 bytes)R and  g(x) = sqrtx3.jpg (756 bytes) for all xin.jpg (595 bytes)R. Is f = g? Explain your answer.

b) Define functions f : Rimplies.jpg (563 bytes)R and g : Rimplies.jpg (563 bytes)R, where   f(x) = x for all  xin.jpg (595 bytes)R and  g(x) = sqrtx2.jpg (796 bytes) for all xin.jpg (595 bytes)R. Is f = g? Explain your answer.

Hint
Full solution

4. Write the sequence  -4, 9, -16, 25, ...  as a function.

Hint
Full solution

5. Read Example 7.1.11 on pages 351 - 352 of the textbook. Then use the Hamming distance function to calculate H(1100101, 0010111).

Hint
Full solution

6. A binary operation on a set X is a special kind of function from X × X to X. One example of a binary operation is addition on the set Z.
Let  f: Z × Z implies.jpg (563 bytes)Z   be the function of addition on the integers.

a) Evaluate f((3,2)).
b) Find an element of Z × Z with an image of  -1.

Hint
Full solution

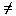7. Suppose you are told that a function  f: Q implies.jpg (563 bytes)Z   is to be defined by the formula f( m/n) = n for all integers m and n where n noteq.jpg (604 bytes) 0. Is f well-defined? Justify your answer.

Hint
Full solution

 

Section 7.2 

Application: Finite-State Automata

The following solutions make use of information found on pages 357 - 364 of the textbook.

Exercise 7.2.1:  Definitions

Fill in the blanks to complete the following sentences.

  1. A finite-state automaton A consists of five objects:
    1. a set I of input symbols, called the input alphabet;
    2. a set S of states in which the automaton can be;
    3. a designated state s0, called the initial state;
    4. a designated set of states called the set of accepting states;
    5. a next-state function  N: S × I implies.jpg (563 bytes) S that associates a "next-state" to each ordered pair consisting of a "current state" and a "current input". For each state s in S and input symbol m in I,  N(s,m) is the state to which A goes if m is input to A when A is in state s.
  2. A (state-)transition diagram is often used to describe the operation of a finite-state automaton. It shows the transitions the machine makes from one state to another in response to various inputs.
  3. A next-state table for an automaton shows the values of the next-state function N for all possible states s and input symbols i.
  4. Let A be a finite-state automaton and let I be the input alphabet. Let I* denote the set of strings over the alphabet I, and let w in.jpg (563 bytes) I*; that is, let w be a string consisting of symbols chosen from the alphabet I. Then w is accepted by A if, and only if, A goes to an accepting state when the symbols of w are input to A in sequence starting when A is in its initial state.
    The language accepted by A, denoted L(A), is the set of all strings that are accepted by A.
  5. Let A be a finite-state automaton with set of states S and input alphabet I. Let I* denote the set of strings over the alphabet I and N: S × I implies.jpg (563 bytes)S denote the next-state function. Then the eventual-state function  N*: S × I* implies.jpg (563 bytes) S is defined as follows:
    For any state s and for any input string w,  N*(s,w) = the state to which A goes if the symbols of w are input to A in sequence starting when A is in state s.

Exercise 7.2.2:  Examples

You should attempt all these exercises yourself, using the textbook as an aid. Once you have attempted each question, check your answers by following the appropriate links. If you are stuck on a question, choose the link that gives you a hint and then try the question again.

1. A vending machine dispenses jaw-breakers that cost 20¢ each. The machine accepts 5¢, 10¢ and 20¢  pieces only and does not give change. As soon as the amount deposited equals or exceeds 20¢, the machine releases a jaw-breaker. The next coin deposited starts (from zero) the process over again.
Draw a transition diagram for this finite-state automaton.

Hint
Full solution

2. Consider the finite-state automaton A defined by the transition diagram below:

S7_2_2.jpg (8995 bytes)

a) What are the states of A? 
b) What are the input symbols of A? 
c) What is the initial state of A? 
d) What are the accepting states of A? 
e) Find N(t1, 1) and N(t3, 0). 
f) Create the annotated next-state table for A.

Hint
Full solution

3. Consider the finite-state automaton A defined by the following next-state table:
S7_2_3.jpg (5353 bytes)

a) What are the states of A? 
b) What are the input symbols of A? 
c) What is the initial state of A?
d) What are the accepting states of A? 
e) Find N(X, b) and N(Y, a). 
f) Draw the transition diagram for A.

Hint
Full solution

4. Refer back to Question 2.
a) To which states would the automaton go for each of the following strings of input symbols?

i) 01       ii) 0010      iii) 11000      iv) 111

b) Which of the strings from part a) send the automaton to an accepting state?

c) What is the language accepted by this automaton?

Hint
Full solution

5. Refer again to Question 2. Find N*(t2, 00100).

Hint
Full solution

Section 7.3 

One-to-One and Onto, Inverse Functions

The following solutions make use of information found on pages 369 - 384 of the textbook.

Exercise 7.3.1:  Definitions

Fill in the blanks to complete the following sentences.

  1. Let F be a function from a set X to a set Y. F is one-to-one (or injective) if, and only if, for all elements x1 and x2 in X, if F(x1) = F(x2), then x1 = x2.
    The contrapositive statement is: " x1, x2 inred.jpg (890 bytes)X, if x1noteqred.jpg (905 bytes)x2, then F(x1)noteqred.jpg (905 bytes)F(x2).
  2. A function  F: Ximplies.jpg (563 bytes)Y is  not one-to-one if, and only if, $ x1, x2 in X such that F(x1) = F(x2) and  x1noteqred.jpg (905 bytes) x2.

    onetoone.jpg (7860 bytes)

    onetooneno.jpg (7563 bytes)
  3. To show that a function f: Ximplies.jpg (563 bytes)Y is one-to-one, you usually suppose that x1 and x2 are elements of X such that f(x1) = f(x2) and show that x1 = x2.
  4. To show that a function f: Ximplies.jpg (563 bytes)Y is not one-to-one, you usually find elements x1 and x2 in X so that f(x1) = f(x2) but x1noteqred.jpg (905 bytes)x2.
  5. Let F be a function from a set X to a set Y. F is onto (or surjective) if, and only if, " y in Y, $ x in X such that y = F(x).
    That is, for all y in Y there exists an x in X such that y is the image of x under F
  6. A function F: Ximplies.jpg (563 bytes)Y is  not onto if, and only if, $ y in Y such that " x in X, F(x)noteqred.jpg (905 bytes)y.

    onto.jpg (7090 bytes)

    ontono.jpg (7568 bytes)
  7. To show that a function f: Ximplies.jpg (563 bytes)Y is onto, you usually suppose that y is an arbitrary element of Y and show that there is an element x in X such that f(x) = y.
  8. To show that a function  f: Ximplies.jpg (563 bytes)Y is not onto, you usually find an element y in Y such that ynoteqred.jpg (905 bytes)f(x) for any x in X.
  9. A one-to-one correspondence (or bijection) from a set X to a set Y is a function F: Ximpliesred.jpg (864 bytes)Y that is both one-to-one and onto.
  10. Suppose that the function F: Ximplies.jpg (563 bytes)Y is both one-to-one and onto; that is, F is a one-to-one correspondence from X to Y.
    Then there exists a function F-1: Yimplies.jpg (563 bytes)X such that for any element y in Y,
    F-1(y) = the unique element x in X such that F(x) = y.
    The function F-1 is called the inverse function for F.
  11. Given a function F: Ximplies.jpg (563 bytes)Y, for which there exists an inverse function F-1: Yimplies.jpg (563 bytes)X, then F-1(y) = x  iff.jpg (928 bytes) y = F(x).

Exercise 7.3.2:  Examples

You should attempt all these exercises yourself, using the textbook as an aid. Once you have attempted each question, check your answers by following the appropriate links. If you are stuck on a question, choose the link that gives you a hint and then try the question again.

1. Which of the following functions are one-to-one? Which of them are onto?

S7_3_1.jpg (26776 bytes)

Hint
Full solution

2. Define the functions f: Rimplies.jpg (563 bytes)R and  g: Rimplies.jpg (563 bytes)R   by  f(x) = | x | + 1 and  g(x) = 2x3-1, for all  x in R. Are these functions one-to-one? In each case either prove that the function is one-to-one or give a counterexample to show that it is not one-to-one.

Hint
Full solution

3. Searching through long lists is a slow process. One way to speed up the search is to divide the long list into a number of smaller lists. If we have some method of quickly identifying in which of the smaller lists a particular item will appear, then we need only search through the smaller list to find the item.

Suppose we wish to maintain the customer records for a large company and begin by assigning each customer a unique 7-digit account number. This 7-digit number will be used as input to a function H which will determine the sublist to be searched to find the account details.  The company has 30,000 customers and we are going to partition the list of accounts into 100 sublists of approximately 300 items each. We define a hash function which maps each 7-digit account number, say n, to an element x in the set {0, 1, 2, 3, ..., 99}, such that  H(n) = x,  where n mod 100 = x.

a) Calculate to which sublists each of the following account numbers would be allocated.
i) 2473871      ii) 3569842      iii) 9085000      iv) 8574642

b) Is the function H one-to-one? Explain.

Hint
Full solution

4. Define the functions F: Rimplies.jpg (563 bytes)R+ È {0} and  G: Zimplies.jpg (563 bytes)Z   by F(x) = x2 for all x in R  and G(x) = x2 for all x in Z. Are these functions onto? In each case either prove that the function is onto or give a counterexample to show that it is not onto.

Hint
Full solution

5. Define the function F: Rimplies.jpg (563 bytes)R by  F(x) = 2x + 4  for all  x in R.  Show that F is onto.

Hint
Full solution


6. Is the function f:  Ximplies.jpg (563 bytes)Y a one-to-one correspondence, where X = {0, 1, 2, 3} and Y = {0, 1, 4, 9} and f(x) = x2  for all x in X? Justify your answer.

Hint
Full solution

7. Given the functions f and g illustrated in the following arrow diagrams, find (if they exist) f-1 and g-1. If they do exist, draw their arrow diagram.

S7_3_7.jpg (14081 bytes)

Hint
Full solution


8. Find (if it exists) the inverse of the function g: Rimplies.jpg (563 bytes)R   where  g(x) = 2x + 5 for all x in R.

Hint
Full solution

Section 7.4 

Application: The Pigeonhole Principle

The following solutions make use of information found on pages 387 - 399 of the textbook.

Exercise 7.4.1:  Definitions

Fill in the blanks to complete the following sentences.

  1. Recall that for a set A, n(A) denotes the number of elements in set A.
  2. Pigeonhole Principle:
    A function, f, from the set X to the set Y, where n(X) > n(Y),  cannot be one-to-one. There must be at least two elements in the domain that have the same image in the co-domain.
  3. Generalized Pigeonhole Principle:
    Let k be a positive integer and f a function from a finite set X to a finite set Y. If n(X) > k · n(Y), then there is some y in Y such that y is the image of at least k + 1 distinct elements of X.
  4. A set is called finite if, and only if, it is the empty set or there is a one-to-one correspondence from {1, 2, 3, ..., n} to the set, where n is a positive integer.
    In the first case, the number of elements in the set is zero, and in the second case it is n.
    A set that is not finite is called infinite.
  5. Theorem   Pigeonhole Principle
    For any function f from a finite set X to a finite set Y, if n(X) > n(Y), then f is not one-to-one.
  6. Theorem: Let X and Y be finite sets with the same number of elements and suppose f is a function from X to Y. Then f is one-to-one if, and only if, f is onto.

Exercise 7.4.2: Examples

You should attempt all these exercises yourself, using the textbook as an aid. Once you have attempted each question, check your answers by following the appropriate links. If you are stuck on a question, choose the link that gives you a hint and then try the question again.

1. How many students must be in a class to guarantee that at least two students receive the same mark on the final exam which is graded on a scale of 0 to 100, (with no half marks allowed)?

Hint
Full solution

2. There are 680 people on a list. Must there be at least two people on the list with the same first and last initials? Justify your answer.

Hint
Full solution

3. The Prime Minister is packing to go to an important meeting in Asia, but there is a sudden black-out and so he is fumbling around in the dark. He is reaching into his wardrobe to find a tie to wear at the meeting. He has 12 ties, five ties that he likes and seven that he doesn't like. How many ties must he pull out of his wardrobe to be guaranteed of having at least one tie that he likes?

Full solution

4. Show that in a group of 25 people, at least three must have the same astrological star sign.

Hint
Full solution

5. Assume that in a group of six people, each pair of individuals are either friends or enemies. Show that there are either three mutual friends or three mutual enemies in the group.

Hint
Full solution

Section 7.5

Composition of Functions

The following solutions make use of information found on pages 401 - 410 of the textbook.

Exercise 7.5.1:  Definitions

Fill in the blanks to complete the following sentences.

  1. Let f: Ximplies.jpg (563 bytes)Y and g: Yimplies.jpg (563 bytes)Z be functions with the property that the range of f is a subset of the domain of g. Define a new function  g o f: Ximplies.jpg (563 bytes)Z as follows:
    (g o f )(x) = g( f (x) )  for all x in X.
    The function g o f is called the composition of  f and g.
    We read g o f as "g circle f " and g( f (x) ) as "g of  f of x".
    Label the following diagram to illustrate the function  g o f.
    S7_5_def.jpg (13392 bytes)
  2. Theorem:
    Let f be a one-to-one correspondence from a set X to a set Y. Then the inverse function exists and can be denoted by f-1: Yimplies.jpg (563 bytes)X. It follows that
    f -1 o f = iX  and  f o f -1 = iY.

Exercise 7.5.2:  Examples

You should attempt all these exercises yourself, using the textbook as an aid. Once you have attempted each question, check your answers by following the appropriate links. If you are stuck on a question, choose the link that gives you a hint and then try the question again.

1. Let f: Rimplies.jpg (563 bytes)R  be defined by f(x) = x3 for all   xin.jpg (595 bytes)R and let g: Rimplies.jpg (563 bytes)R be defined by g(x) = 2x - x2  for all  xin.jpg (595 bytes)R.

a) Find (f o g)(x) and (g o f)(x). 

b) Is  g o f = f o g?

Hint
Full solution


2. Let X = {a, b, c},  Y' = {1, 2, 3}, Y = {1, 2, 3, 4} and Z = {w, x, y, z}. Define the functions  f: Ximplies.jpg (563 bytes)Y' and  g: Yimplies.jpg (563 bytes)Z by the diagram below.

S7_5_2.jpg (11986 bytes)

a) Draw the arrow diagram for g o f.
b) What is the range of g o f?

Hint
Full solution

3. Suppose that f: Zimplies.jpg (563 bytes)Z is a function where f (x) = x + 1 for all xin.jpg (595 bytes)Z. Let iZ be the identity function.

a) Find  ( f o iZ )(x) and ( iZ o f )(x).

b) If  g: Ximplies.jpg (563 bytes)X  is any function, what can you say about the functions  g o iX and iX o g?

Hint
Full solution

4. Let f and g be functions defined by the arrow diagrams below.

S7_5_4.jpg (11657 bytes)

a) Draw the arrow diagram representing g o f.
b) f and g are both one-to-one. Is g o f  one-to-one?

Hint
Full solution

5. Let F and G be functions defined by the arrow diagrams below.

S7_5_5.jpg (11048 bytes)

a) Draw the arrow diagram representing F o G.
b) F and G are both onto. Is F o G onto?

Hint
Full solution

Section 7.6 

The Cardinality of a Set (Extension Material)

The following solutions make use of information found on pages 411 - 416 of the textbook.

Exercise 7.6.1:  Definitions

Fill in the blanks to complete the following sentences.

  1. Recall that a finite set is either the empty set or a set that has a one-to-one correspondence with a set of the form {1, 2, 3, ..., n} for some positive integer n.
    An infinite set is a nonempty set that cannot be put into one-to-one correspondence with the set {1, 2, 3, ..., n} for any positive integer n.
  2. Let A and B be any sets.  Sets A and B are said to have the same cardinality if, and only if, there is a one-to-one correspondence from A to B.
    In other words, A has the same cardinality as B if, and only if, there is a function from A to B that is one-to-one and onto.
  3. A set is said to be countably infinite if, and only if, it has the same cardinality as the set of positive integers Z+.
    A set is said to be countable if, and only if, it is finite or countably infinite.
    A set that is not countable is said to be uncountable.
  4. Recall that a function from one finite set to another set of the same size is one-to-one if, and only if, it is onto. 
    This result does not hold for infinite sets.

Exercise 7.6.2:  Examples

You should attempt all these exercises yourself, using the textbook as an aid. Once you have attempted each question, check your answers by following the appropriate links. If you are stuck on a question, choose the link that gives you a hint and then try the question again.

1. Show that the set of all odd integers is countable.

Hint
Full solution

2. Show that there is no one-to-one correspondence between a set X and its power set   P(X).

Hint
Full solution

3. Verify that the set P(Z+) is uncountable.

Hint
Full solution



Back to workbook solution page