3. a) There are at least two ways to approach this problem.
Solution 1: We shall combine the facts that a tree with p vertices has p-1 edges and that the sum of the degrees of any graph is equal to twice the number of edges. Hence
p |
deg(vi) | = |
2(p-1) | |
| S | ||||
| i=1 | ||||
5 + 1 + 1 + 1 + 1 + 1 + |
p-6 |
deg(vi) | = |
2p - 2 |
| S | ||||
| i=1 | ||||
| p-6 | deg(vi) | = |
2p - 12 | |
| S | ||||
| i=1 | ||||
the sum of the degrees of p-6 vertices |
= |
2(p - 6) | ||
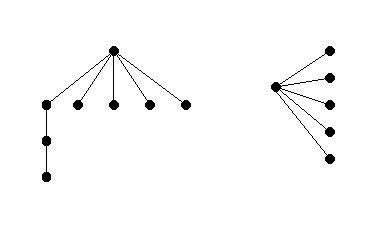
Now we know that none of the remaining p-6 vertices have degree 0 or 1, so they must all have degree 2.
Solution 2: Alternately, we can think about the paths from the vertex of degree 5 to the vertices of degree 1 (the leaves of the tree) and whether or not these paths can branch out. If these paths branched at any point, then either we would get more than 5 vertices of degree 1, or the branching path would have to join one of the other paths which would create a circuit. Since we know we have a tree with exactly 5 vertices of degree 1 and we know that trees do not contain circuits, none of the paths from the vertex of degree 5 to the leaves of the tree can branch. Hence, all the remaining p-6 vertices must have degree 2.
b) There are many different such trees on 8 vertices, but only one on 6 vertices.
