Protect or Create?
One of the most pressing questions for modern conservation biologists is to preserve the populations of endangered species that have been forced to occupy patches of subdivided habitat. One such population is the greater bilby (Macrotis lagotis).

The bilby is a type of bandicoot that was once distributed over 70% of the arid and semi-arid regions of Australia, but is now largely restricted to parts of the Tanami Desert in the Northern Territory, the Gibson and Great Sandy Deserts of Western Australia and one isolated population, consisting of four patches, between Boulia and Birdsville in south-western Queensland. The decline in the bilby’s range is a result of habitat destruction by cattle and rabbits, as well as from predation by cats, dingoes and foxes.
Possible management options available for protecting this species are: 1) to create new patches of habitat suitable for bilby occupancy, and subsequently translocate bilbies to these patches, or 2) to protect the existing patches from habitat destruction and predation. Consequently, we are left with the question – protect or create?
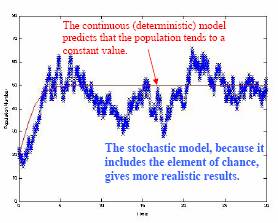
Obviously the optimal choice will depend upon a number of factors, such as: the average life-span of a bilby, how often the bilby gives birth and migrates between patches, how often cattle and rabbits destroy the habitat, and how often predation occurs. Thus, in order to determine the optimal decision, we need to create a mathematical model that describes the dynamics of the bilby population and the influence of these other factors on population dynamics. The model that has been developed is a probabilistic model, since each of the events of interest is governed by chance. In particular we use a Markov chain. This is a stochastic model that satisfies the Markov property: the state of the process at a future time depends only upon the current state of the process. This is often summarised by the expression that a Markov chain is “memoryless”. The stochastic model (blue crosses) provides a much more accurate model of the system than the traditional (deterministic) model (red line), because it incorporates fluctuations in the population due to chance events.
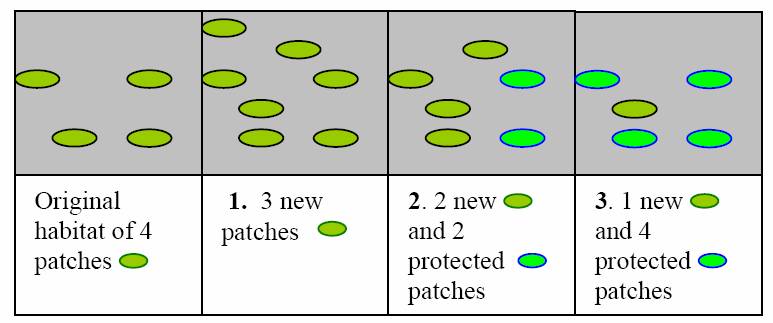
As always, there are budget constraints. Consider the bilby population inhabiting south-western Queensland. Assume it costs $4 million to construct a new patch of habitat, $100,000 per patch per year to protect a patch from destruction and predation, and we are given a 20 year budget of $12 million. Then starting with 4 existing patches, the 3 most obvious management options are: 1. Create 3 new patches. 2. Create 2 new patches and protect 2 patches. 3. Create 1 new patch and protect 4 patches.
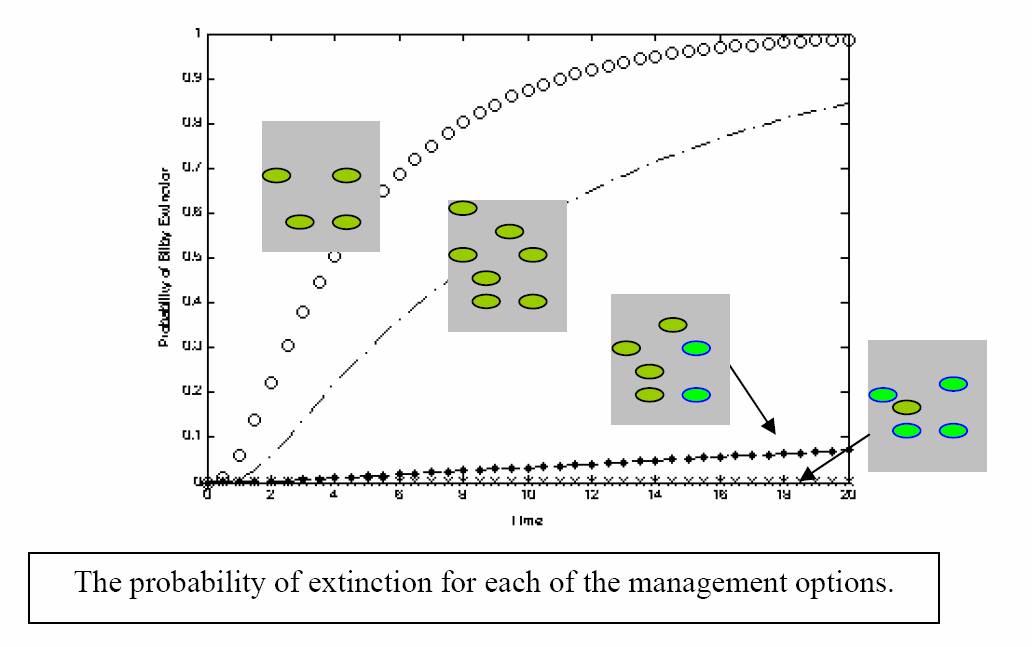
The stochastic model we have developed allows us to incorporate the probabilities of events that impact on the bilby population and, given a particular management option, it returns a probability of extinction of the bilby population. The results for the 4 management options described above are shown in the graph below.
The figure shows that the optimal management strategy to prolong the species over the next 20 years is to create 1 new patch of habitat and protect 4 of the five patches. This will result in the probability of extinction decreasing from almost 1 (that is, almost certain death for the bilby without any intervention) to 0.002, or less than a 1% chance of extinction.
This result highlights the importance of mathematical modelling in determining optimal management strategies. The natural instinct, when faced with attempting to prolong a species existence, would be to make more patches of habitat and translocate the species to these patches. However, our investigation has shown that the optimal strategy in this particular case is to protect the existing patches from habitat destruction and predation before creating new patches.
Joshua Ross is a research student in mathematics at the University of Queensland. The model and software mentioned above have been developed in association with Professor Phil Pollett, Professor Hugh Possingham and fellow research student David Sirl.
