Evolutionary Algorithm Problem 112

This is a test example originally from [4], problem 112 on pg 121. The nonlinear programming problem is to find $\mathbf{x}$ so as to minimize the objective function:

$$f(x)= \sum_{j=1}^{10} x_j (c_j + \ln \frac{x_j}{x_1 + \ldots + x_{10}}),$$

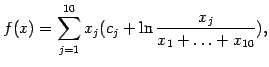
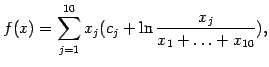
subject to the constraints:

$x_1 + 2x_2 + 2x_3 + x_6 + x_{10} - 2 = 0$

$x_4 + 2x_5 + x_6 + x_7 -1 = 0$

$x_3 + x_7 + x_8 + 2x_9 + x_{10} = 0$

$x_i \ge 0.000001 (i=1, \ldots, 10)$ ,

where

$c_1=-6.089; c_2=-17.164; c_3=-34.054; c_4=-5.914; c_5=-24.721;$

$c_6=-14.986; c_7=-24.100; c_8=-10.708; c_9=-26.662; c_{10}=-22.179$ .

The previous best known solution in [4] was

$\mathbf{x}^{*} = (.01773548, .08200180, .8825646, .0007233256, .4907851$

             $.0004335469, .01727298, .007765639, .01984929, .05269826)$ ,

and $f(\mathbf{x}^{*}) = -47.707579$ .

GENECOP (GEnetic algorithm for Numerical Optimization for COnstrained Problems) in [5] was able to obtain better values for all the points above in all ten runs, and the best solution found was

$\mathbf{x}^{*} = (.04034785, .15386976, .77497089, .00167479, .48468539,$

             $.00068965, .02826479, .01849179, .03849563, .10128126)$ ,

and $f(\mathbf{x}^{*}) = -47.760765$ . A single run of 1000 iterations took 56 sec of CPU time.

In order to condition the CE method to apply on problems with constraints, the techniques which were used in GENECOP for handling constraints are improvised into the CE algorithm. We take advantage of the independence of the three equalities equations and reduce the original problem of ten variables to that of three variables $x_1, x_4$ and $x_8$ . These three variables are expressed as functions in terms of the remaining seven variables which can be seen in gen.m as original equalities.

The next step is just to minimize the search space by setting a domain for each variable. We can estimate the feasible range $\langle \emph{left}(k), \emph{right}(k) \rangle$ for each variable $\mathbf{x}_{k}$ , $k=1, \ldots,10$ , from the constraints equations. After running the CE algorithm once, we can update the domains of the variables from the solution obtained.

The CE algorithm manages to yield better performances than the previous two mentioned above. The optimal solution found was

$\mathbf{x}^{*} = (.0406704399867019, .147751405313913, .783127618406918$ ,

         $.0014144814371999, .485239376708956, .000693320401560864$ ,

         $.0274134447433275, .0179476250414884, .0.037316559819095$ ,

         $.0968781921700762)$ ,

and $f(\mathbf{x}^{*}) = -47.7610908533872$ . The CE parameters were ssample size $m=75$ , rarity parameter $\varrho =0.2$ and smoothing parameter $\alpha=0.3$ . By the 35th iteration, the solution obtained was already better than the best solution of GENECOP. This result was derived after 201 iterations in 365 sec of CPU time.

gen.m - generation of samples, satifying constraints.

normt1.m - generates truncated normals

opt.m - main program

S.m - objective function