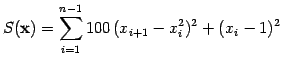 |
(1) |
The test programs below are all run via one CE program: CEoptima.m
The following is a batchfile to run the programs: runTHIS.m
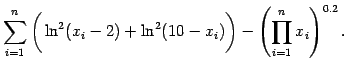 |
(3) |
| (4) |
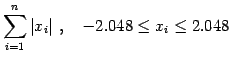 |
(5) |
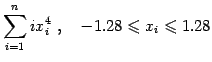 |
(6) |
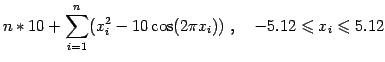 |
(7) |
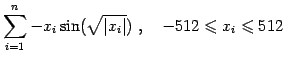 |
(8) |
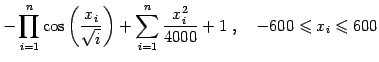 |
(9) |
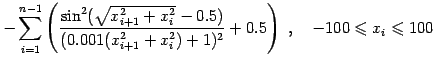 |
(10) |
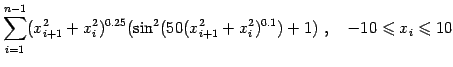 |
(11) |
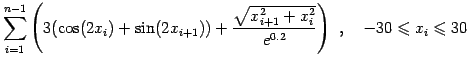 |
(12) |
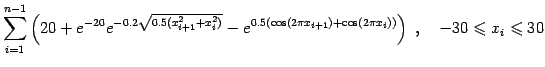 |
(13) |
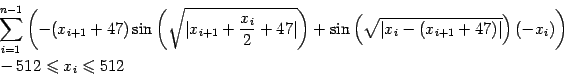 |
(14) |
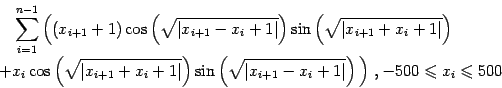 |
(15) |
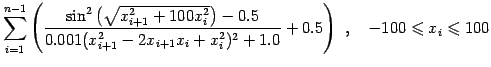 |
(16) |
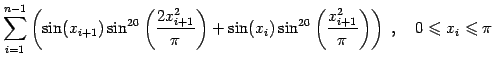 |
(17) |
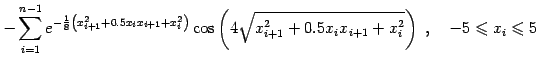 |
(18) |
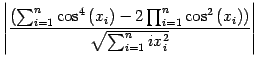 |
(19) |
Constraints:
![]() .
.
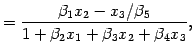
where the betas are the unknown parameters, and the xs are the input variables. The parameters are estimated via the least squares criterion. That is, the parameters are such that the sum of the squared differences between the observed responses and their fitted values of rate is minimized. The following input data are used: