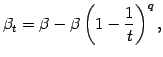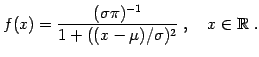- Injection. The idea behind the injection modification, first
proposed
in [2], is to inject extra variance
into the sampling distribution in order to avoid premature ``shrinkage''
of the distribution. More precisely,
let Sstar denote the best performance found at some iteration
t, and
sigstar the largest standard deviation at that iteration.
If sigstar is sufficiently small, and Ssdiff = |Sstar(t) -
Sstar(t-1)|
is also small, then add a constant times Ssdiff to each standard
deviation, for some fixed constant, say 1 - 100.
- Increasing
 , decreasing
, decreasing 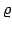 . This is a basic
idea to increase the accuracy. One simply increases the sample size,
while, possibly, decreasing the rarity parameter.
Alternatively, the sample size is increased while the elite sample
size is kept constant. A more sophisticated approach is given by the
FACE algorithm.
. This is a basic
idea to increase the accuracy. One simply increases the sample size,
while, possibly, decreasing the rarity parameter.
Alternatively, the sample size is increased while the elite sample
size is kept constant. A more sophisticated approach is given by the
FACE algorithm.
- Modified or dynamic smoothing.
When the
smoothing parameter alpha is large, say 0.9, the convergence to a
degenerate distribution may happen too quickly, which would ``freeze'' the
algorithm in a sub-optimal solution. One way to prevent this from
happening is to use dynamic smoothing [6] where
at iteration t the variance of the normal sampling distribution
is updated using a smoothing parameter
where q is a small integer (typically between 5 and 10) and
beta is a large smoothing constant (typically between 0.8 and 0.99).
The mean parameter can be updated in the conventional way, with
constant smoothing parameter.
By using a time dependent smoothing parameter the speed of convergence to the
degenerate case is polynomial instead of exponential.
A difficulty with dynamic smoothing is that when the optimal
function value is unknown it is difficult to formulate a good
stopping criterion due to the slower convergence of the algorithm
- Heavy-tailed sampling. Instead of the usual normal sampling
distribution, one could use a distribution with a heavier tail, such
as the Cachy distribution with location parameter mu and
scale
parameter sigma. That is, with pdf
The advantages are that (1) injection or dynamic smoothing may not be
necessary, (2) generation from a Cauchy distribution and also a
truncated Cauchy distribution is
easy.
A disadvantage is that the maximum likelihood estimators for mu
and sigma are not
easily derived. However, the median of the data and the range
(maximum - minumum) are accurate estimators of the location and
scale parameters, respectively.
cetoolbox www user
2004-12-17